 Fourier Series: Basic Results
Fourier Series: Basic Results Fourier Series: Basic Results
Fourier Series: Basic Results
Recall that the mathematical expression
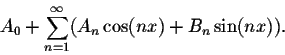
Definition. A Fourier polynomial is an expression of the form
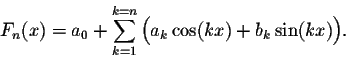
The Fourier polynomials are ![]() -periodic functions. Using the trigonometric identities
-periodic functions. Using the trigonometric identities
![\begin{displaymath}\begin{array}{lcr}
\sin(mx)\cos(nx) &=&\displaystyle \frac{1}...
...e \frac{1}{2}\Big[\cos((m-n)x) - \cos((m+n)x) \Big]
\end{array}\end{displaymath}](img6.gif)
Using the above formulas, we can easily deduce the following result:
Theorem. Let
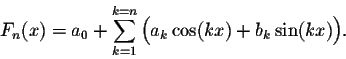
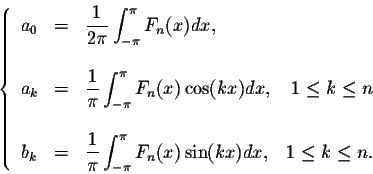
This theorem helps associate a Fourier series to any ![]() -periodic function.
-periodic function.
Definition. Let f(x) be a ![]() -periodic function which is integrable on
-periodic function which is integrable on
![]() .
Set
.
Set
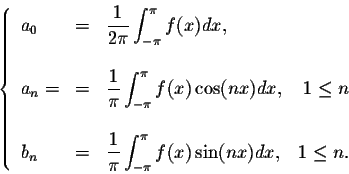
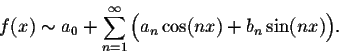
Example. Find the Fourier series of the function
![\begin{displaymath}b_n = \frac{1}{\pi} \int_{-\pi}^{\pi} x \sin(nx)dx =
\frac{1...
...\frac{x\cos(nx)}{n} + \frac{\sin(nx)}{n^2}\right]^{\pi}_{-\pi}.\end{displaymath}](img22.gif)
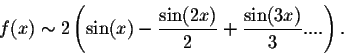
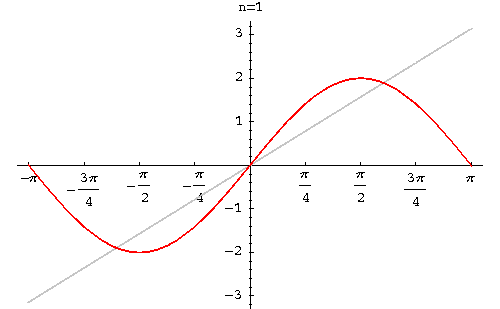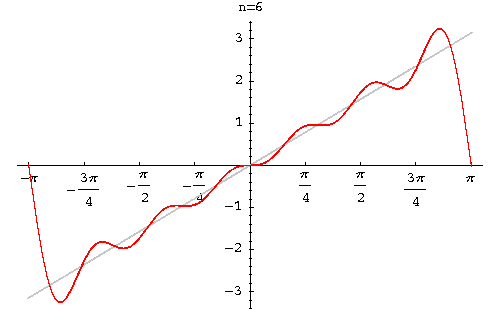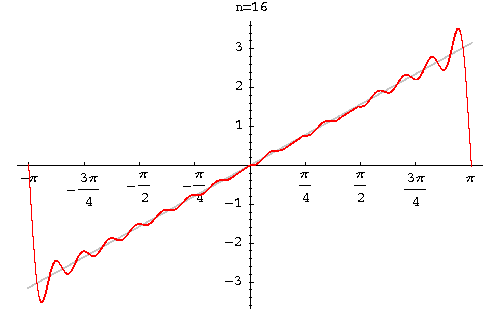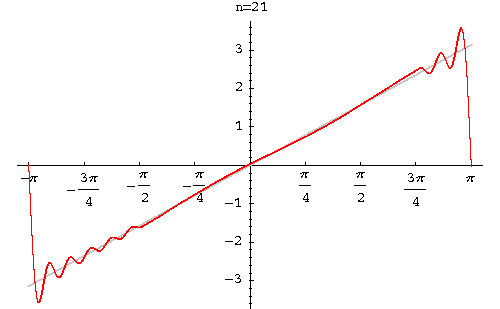
|
Example. Find the Fourier series of the function
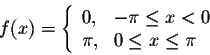
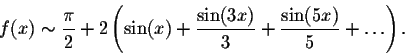
|
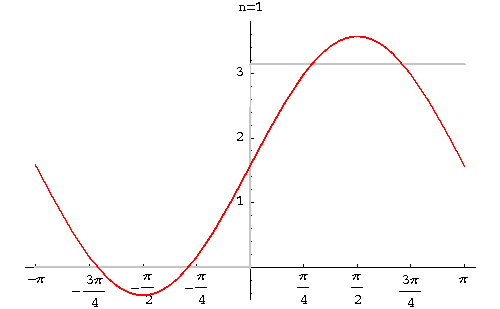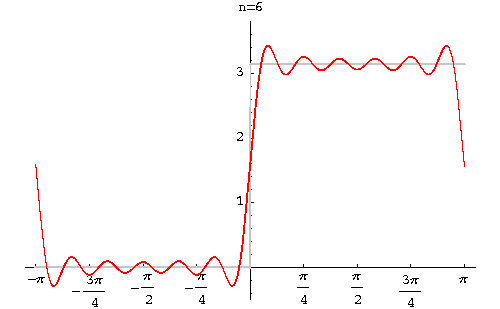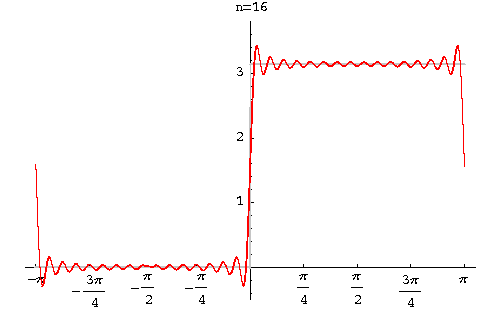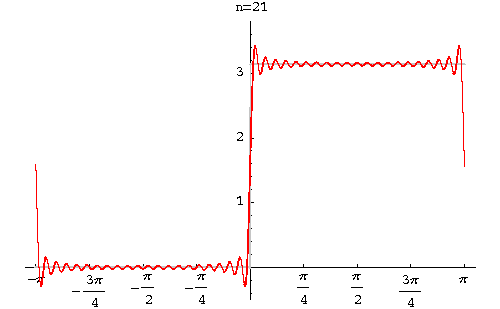
Example. Find the Fourier series of the function
function
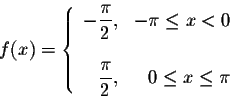
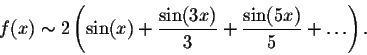
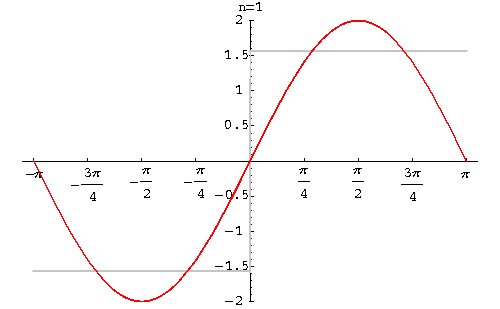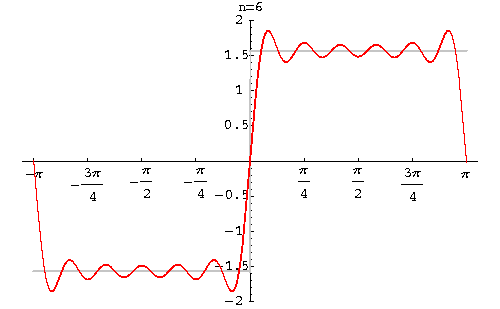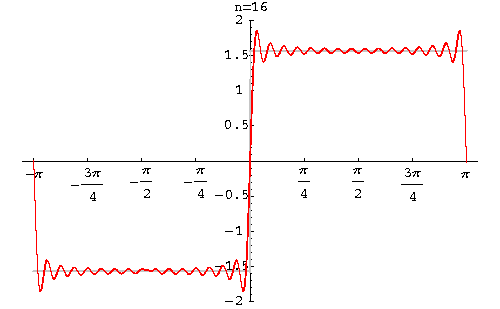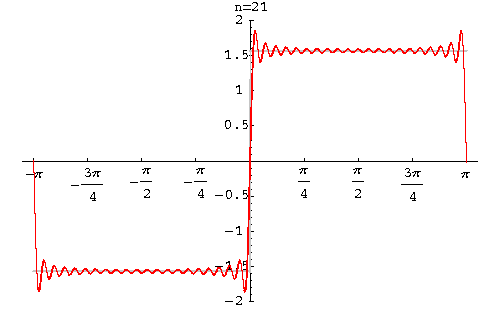
|
Remark. We defined the Fourier series for functions which are ![]() -periodic, one would wonder how to define a similar notion for functions which are L-periodic.
-periodic, one would wonder how to define a similar notion for functions which are L-periodic.
Assume that f(x) is defined and integrable on the interval [-L,L]. Set
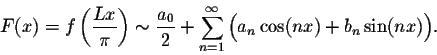
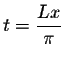 ,
we obtain the following definition:
,
we obtain the following definition:
Definition. Let f(x) be a function defined and integrable on [-L,L]. The Fourier series of f(x) is
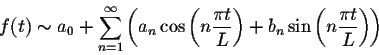
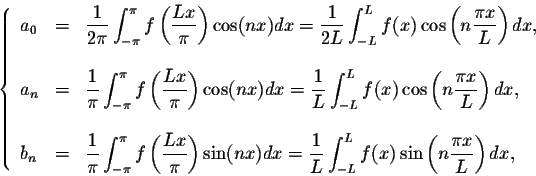
Example. Find the Fourier series of
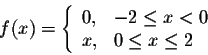
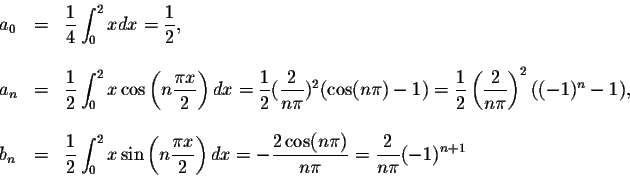
![\begin{displaymath}f(x) \sim \frac{1}{2} +
\sum_{n=1}^{\infty} \left[\frac{2}{n...
...rac{2}{n\pi}(-1)^{n+1}\sin\left(n\frac{\pi x}{2}\right)\right].\end{displaymath}](img41.gif)
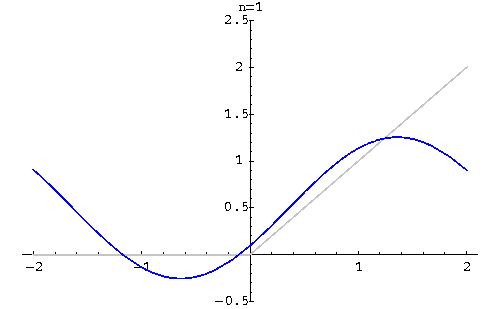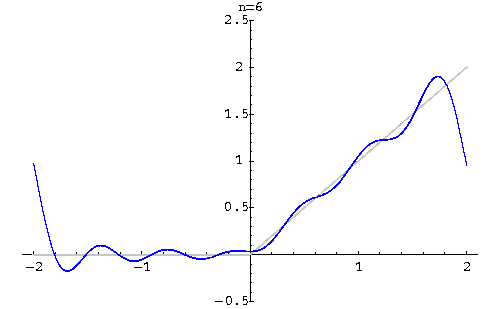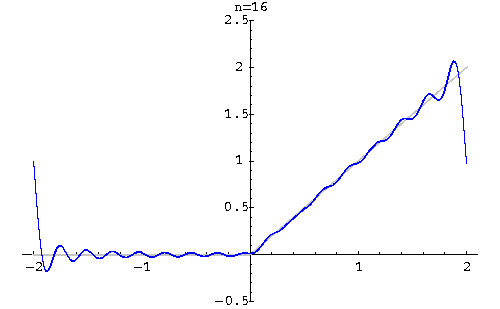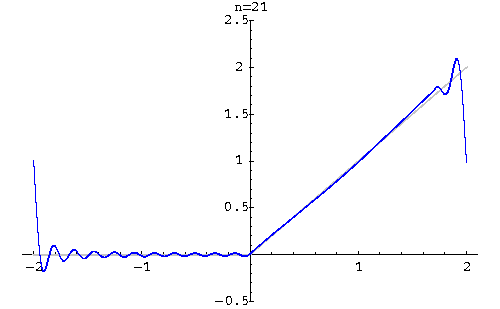
|

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: M.A. Khamsi