Answer to Example 6

Example: Solve the initial value problem

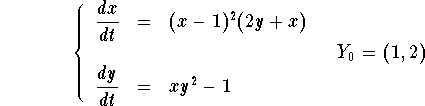
Answer: Notice that for x=1, we have . Hence, the constant function x(t) = 1 is solution to the first equation of the system. Set x=1 in the second equation to get

This is a first order differential equation which is separable. Let us solve it. First, we look for the constant solutions which may be obtained from

We get . The non-constant solutions may be obtained by first separating

,

and then performing the integration

The technique of integration of rational functions gives

,

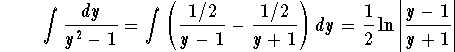which implies

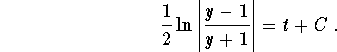
If we set y=2 when t=0, we get

.

Easy algebraic manipulations give

.

Therefore, the solution Y = (x,y), where

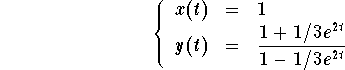
satisfies the initial condition . By the existence and uniqueness theorem, this is the desired solution.

[Differential Equations] [First Order D.E.] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard..

Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour