 Introduction: Example4
Introduction: Example4

Example: Consider the following predator-prey model:
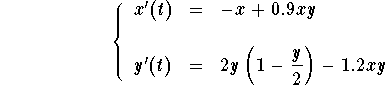 .
.
- 1.
- Does x(t) denote the predator population or the
prey population? Justify your answer.
- 2.
- Find all equilibrium points of the system.
- 3.
- Suppose the prey population becomes extinct while the predator population is still positive. Describe the long-term behavior of the predator population.
- 4.
- Suppose the predator population becomes extinct while the prey population is still positive. Describe the long-term behavior of the prey population.
- 5.
- Describe the long-term behavior of the system when the initial populations are given by
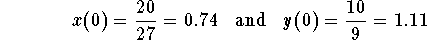 .
.
Solution:
Next Example:

[Differential Equations]
[First Order D.E.]
[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard..

Author:
Mohamed Amine Khamsi
Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Introduction: Example4
Introduction: Example4 Introduction: Example4
Introduction: Example4
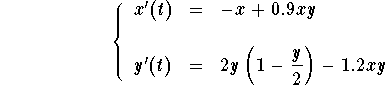 .
.
![]() .
. 
 S.O.S MATHematics home page
S.O.S MATHematics home page 