 Euler's Method: Answer to Example1
Euler's Method: Answer to Example1

Example: Consider the autonomous differential equation with the initial condition
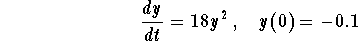 .
.
- 1.
- Find
 .
.
Hint: You may want to sketch the Slope Fields of this differential equation.
- 2.
- Find the first five terms of the Euler Approximation when
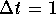 .
.
- 3.
- Is there a contradiction between the results of 1 and 2 ?
If yes, explain what happened.
Answer:
- 1.
- First, let us draw the slope fields of the differential equation.
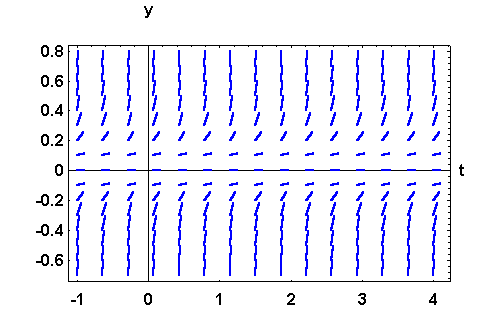
Since 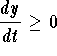 , any solution to the differential equation is increasing. This differential equation has one critical solution y=0. Since the initial condition satisfied by the solution to the IVP is y(0) = -0.1 < 0, then we have y(t) <0 for all t. We deduce from this that
, any solution to the differential equation is increasing. This differential equation has one critical solution y=0. Since the initial condition satisfied by the solution to the IVP is y(0) = -0.1 < 0, then we have y(t) <0 for all t. We deduce from this that

- 2.
- Recall the formula which gives the euler's approximations to the solution
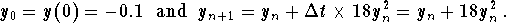
This gives the first five terms as:
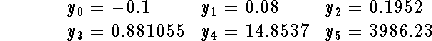
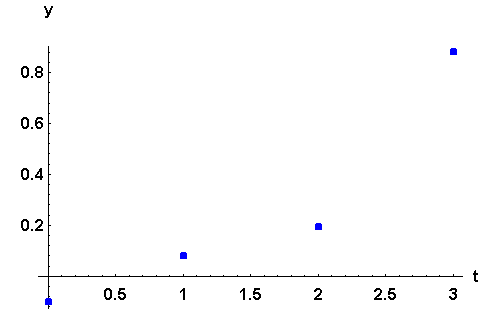
- 3.
- According to the result in Part 1, the solution to the given IVP should always be negative and according to the above Euler's approximation the first term
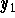 is positive. This is our contradiction. As a matter of fact, according to the slope field, the Euler's approximation should continue to rise and even tend to
is positive. This is our contradiction. As a matter of fact, according to the slope field, the Euler's approximation should continue to rise and even tend to 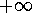 , which even further contradicts the conclusion of 1.
, which even further contradicts the conclusion of 1.
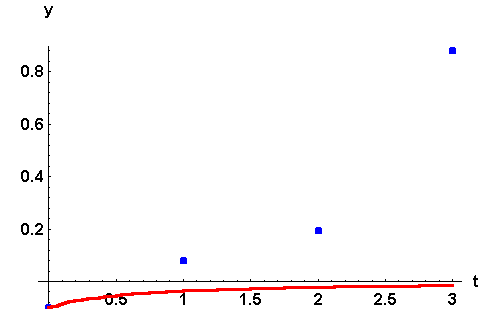
The reason behind this is that 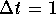 is a large step. So, after the first shot, it shoots above the critical solution y=0. Try to do the same problem with different step-sizes.
is a large step. So, after the first shot, it shoots above the critical solution y=0. Try to do the same problem with different step-sizes.

[Differential Equations]
[Euler's Method]
[Geometry]
[Algebra]
[Trigonometry ]
[Calculus]
[Complex Variables]
[Matrix Algebra]
 S.O.S MATHematics home page
S.O.S MATHematics home page
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.

Author: Mohamed
Amine Khamsi
Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
 Euler's Method: Answer to Example1
Euler's Method: Answer to Example1  Euler's Method: Answer to Example1
Euler's Method: Answer to Example1 
![]() .
. ![]() .
. 
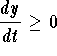 , any solution to the differential equation is increasing. This differential equation has one critical solution y=0. Since the initial condition satisfied by the solution to the IVP is y(0) = -0.1 < 0, then we have y(t) <0 for all t. We deduce from this that
, any solution to the differential equation is increasing. This differential equation has one critical solution y=0. Since the initial condition satisfied by the solution to the IVP is y(0) = -0.1 < 0, then we have y(t) <0 for all t. We deduce from this that
![]()
![]()
![]()


![]() is a large step. So, after the first shot, it shoots above the critical solution y=0. Try to do the same problem with different step-sizes.
is a large step. So, after the first shot, it shoots above the critical solution y=0. Try to do the same problem with different step-sizes.

 S.O.S MATHematics home page
S.O.S MATHematics home page 