Homogeneous Equations

The differential equation

is homogeneous if the function f(x,y) is homogeneous, that is-

Check that the functions

.

are homogeneous.

In order to solve this type of equation we make use of a substitution (as we did in case of Bernoulli equations). Indeed, consider the substitution . If f(x,y) is homogeneous, then we have

Since y' = xz' + z, the equation (H) becomes

which is a separable equation. Once solved, go back to the old variable y via the equation y = x z.

Let us summarize the steps to follow:

(1)

Recognize that your equation is an homogeneous equation; that is, you need to check that f(tx,ty)= f(x,y), meaning that f(tx,ty) is independent of the variable t;

(2)

Write out the substitution z=y/x;

(3)

Through easy differentiation, find the new equation satisfied by the new function z.
You may want to remember the form of the new equation:

(4)

Solve the new equation (which is always separable) to find z;

(5)

Go back to the old function y through the substitution y = x z;

(6)

If you have an IVP, use the initial condition to find the particular solution.

Since you have to solve a separable equation, you must be particularly careful about the constant solutions.

Example: Find all the solutions of

Solution: Follow these steps:

(1)

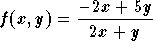It is easy to check that is homogeneous;

(2)

Consider ;

(3)

We have

,

which can be rewritten as

This is a separable equation. If you don't get a separable equation at this point, then your equation is not homogeneous, or something went wrong along the way.

(4)

All solutions are given implicitly by

(5)

Back to the function y, we get

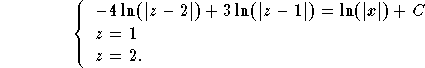
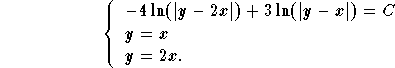
Note that the implicit equation can be rewritten as

[Differential Equations] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S. MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Last Update 6-23-98

Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour