Existence and Uniqueness of Solutions: Example 1

Example: Suppose the differential equation 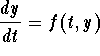satisfies the Existence and Uniqueness Theorem for all values of y and t. Suppose and are two solutions to this differential equation.

1.

What can you say about the behavior of the solution of the solution y(t) satisfying the initial condition y(0)=1?
Hint: Draw the two solutions and .

2.

Address the behavior of y(t) as t approaches , and as t approaches .

Answer:

1.

First let us draw the graphs of and .

Since we have , we deduce from the Existence and Uniqueness Theorem that for all t, we have

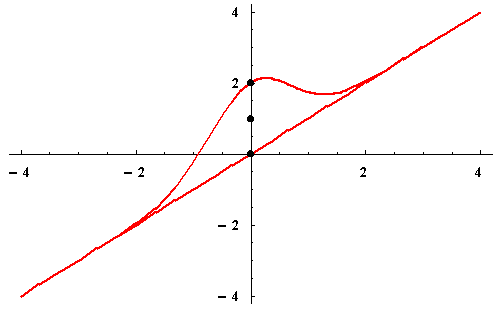In particular, y(t) has the line y=t as an oblique asymptote which answers the second question.

We cannot predict that y(t) is an increasing function.

[Differential Equations] [Slope Field] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour