Bifurcations: Answer to Example 1

Example: Consider the autonomous equation

with parameter a.

1.

Draw the bifurcation diagram for this differential equation.

2.

Find the bifurcation values, and describe how the behavior of the solutions changes close to each bifurcation value.

Answer:

1.

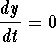First, we need to find the equilibrium points (critical points). They are found by setting . We get

.

This a quadratic equation which solves into

,

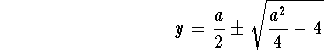we have

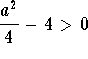• if , then we have two equilibrium points;
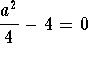• if , then we have one equilibrium point;
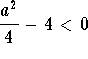• and if , then we have no equilibrium points.

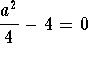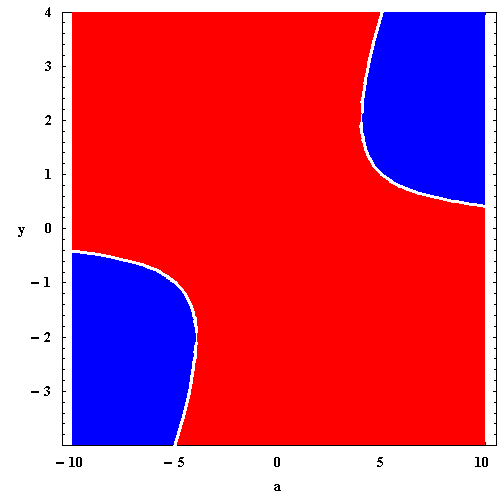
This clearly implies that the bifurcation occurs when , or equivalently , which gives . The bifurcation diagram is given below. The equilibrium points are pictured in white, red colored areas are areas with "up" arrows, and blue colored areas are areas with "down" arrows.

2.

The bifurcation values are a = 4 and a = -4. Let us discuss what is happening around a=4 (similar conclusions hold for the other value):

• Left of a=4: no equilibrium;
• At a=4: we have a node (up), i.e. attractive from below and repelling from above (look at the bifurcation diagram);
• Right of a=4: we have two equilibria, the smaller one is a sink, the bigger one is a source, which explains the node behavior of .

[Differential Equations] [Slope Fields] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S. MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Last Update 6-23-98

Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour