Population Dynamics: Answer to Example1

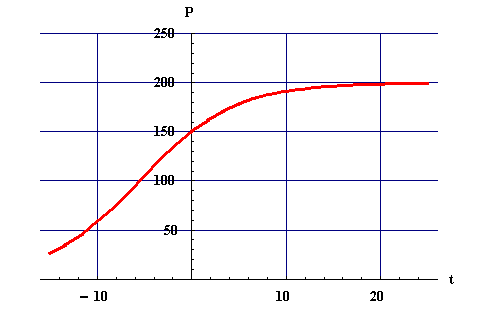
Example: Let P(t) be the population of a certain animal species. Assume that P(t) satisfies the logistic growth equation

1.

Is the above differential equation separable?

2.

Is the differential equation autonomous?

3.

Is the differential equation linear?

4.

Without solving the differential equation, give a sketch of the graph of P(t).

5.

What is the long-term behavior of the population P(t)?

6.

Show that the solution is of the form

Find A and B.
Hint: Use the initial condition and the result of 5.

7.

Where is the solution's inflection point?
Hint: This can be done without using the answer of 6.

8.

What is special about the growth rate of the population P(t) at the inflection point (found in 7)?

Answer:

1.

This differential equation is autonomous, i.e. the variable t is missing. Therefore, this equation is indeed separable.

2.

The answer is Yes! (see 1.) Every autonomous differential equation is separable.

3.

The equation is not linear because of the presence of .

4.

The graph of the solution P(t) is as follows:

5.

Clearly, because of the initial condition (see the graph of the solution below), we have

,

200 being the carrying capacity.

6.

Let us solve this equation (use the technique for solving separable equations). First, we look for the constant solutions (equilibrium points or critical points). We have

Then, the non-constant solutions can be generated by separating the variables

,

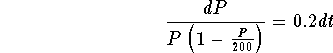and the integration

.

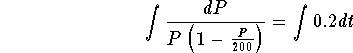Next, the left hand-side can be handled by using the technique of integration of rational functions. We get

,

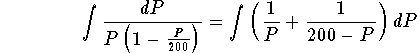which gives

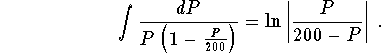
Hence, we have

.

Easy algebraic manipulations give

,

where .
Therefore, all the solutions are

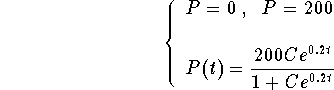
where C is a constant parameter.

Remark: We may rewrite the non-constant solutions as

,

where a and B are two parameters. If we use the conditions

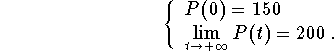
we will be able to get the desired solution. Indeed, we have

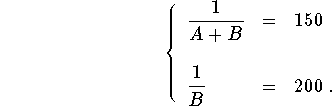
Thus, 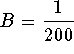and consequently .

7.

From the graph (see 4.), the graph of P(t) has an inflection point between 0 and 200. Let us find it. Since we must have P''(t) = 0, we get

,

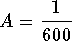where we used the chain rule and the fact that 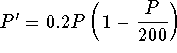. Since our solution is not one of the two constant solutions we are only left with the equation

This simplifies to

,

which gives P=100 (half-way between 0 and 200).

Remark: You still need to convince yourself that t=100 is indeed the inflection point, that is the second derivative changes sign at that point.

8.

The growth rate at t=100 is maximal.

Next Example:

[Differential Equations] [Linear Equations] [Separable Equations] [Geometry] [Algebra] [Trigonometry ] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour