![]()
Answer:
![]()
![]()
Answer:The values of x that make this inequality true are
included on the intervals ![]() .
.
- The distance between the two points.
Answer: The distance is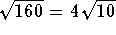 .
.
- The midpoint of the two points.
Answer: The midpoint is (1,2). - The equation of the line between the two points.
Answer:The equation of the line is y=-3x+5. - The equation of the circle whose diameter is the line between
the two points.
Answer: The circle is the locus of the points described by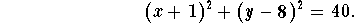
|
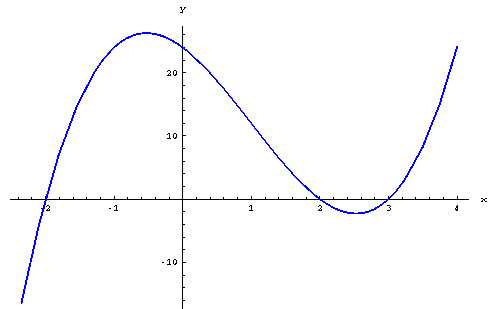
- Approximate the interval(s) where the function is increasing.
Answer: The function is increasing approximately on the intervals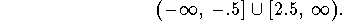
- Approximate the interval(s) where the function is decreasing.
Answer: The function is decreasing approximately on the interval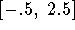 .
. - Approximate the relative maximum value of the function.
Answer:The relative maximum value is about 26.
- Approximate the relative minimum value of the function.
Answer:The relative minimum value is about -2.
- How does the graph of -f(x) differ from the graph of f(x)?
Answer:The graph of -f(x) is reflected about the x-axis. - How does the graph of f(x)+3 differ from the graph of f(x)?
Answer:The graph of f(x)+3 has a vertical shift of 3. - How does the graph of f(x-4)-6 differ from the graph of f(x)?
Answer:The graph of f(x-4)-6 has a vertical shift of -6 and a horizontal shift of 4.
- Find (f+g)(x).
Answer: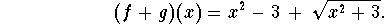
- Find
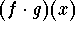 .
.
Answer: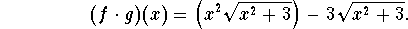
- Find
 .
.
Answer: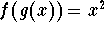 .
.