| Time: 1 hour |
|---|
Problem 1. Find all local maxima and minima of the function
Answer. The critical points are
Since
(1,2,3) and (-1,2,3) are possible candidates for local minima and (0,2,3) is a possible candidate for local maxima. Note that by completing the squares, we get
which implies that (1,2,3) and (-1,2,3) are not only local minima
but global minima. The point (0,2,3) is not a local maxima.
Problem 2. Use the method of Lagrange multipliers to find the point on the line of intersection of the planes
that is the closest to the origin.
Answer. Set
Then by the method of Lagrange multipliers if (x,y,z) is the point which is the closest to the origin, we must have
where 
and 
are real numbers. We get
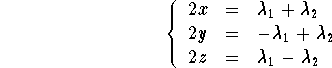
Playing around with the system knowing that x-y+z=4 and x+y-z=8, we get
This leads us to conclude that a good candidate for the minimum of f(x,y,z) is (6,1,-1) with f(6,1,-1)=38. The shortest distance to the origin is therefore
Another way to prove this is to parametrize the line
which gives
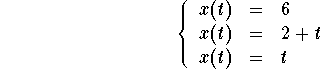
Plug these into f(x,y,z) to find
It is now clear that the minimum is achieved at t=-1 and the minimum value is 38...
Problem 3. Use the method of Lagrange multipliers to find local maxima of
under the constraints
Answer. Set
Then by the method of Lagrange multipliers if (x,y,z) is a local maxima (or minima), we must have
where and are real numbers. We get
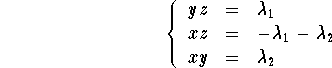
Playing around with the system knowing that x-y=0 and z=y-2, we get
Since
then f(x,y,z) has a local maxima at (0,0,-2). Another way to see this set x=y and z=y-2 in the definition of f. We will get
It is very easy to see that y=0 is a local maxima and y=4/3 is a local minima....
Problem 4. Find the integral of
over the plane region G bounded by the lines y = x, y = -x
and x = 4
Answer. Clearly we have
(see the picture below of the set G)
Therefore, we have
Easy calculations give
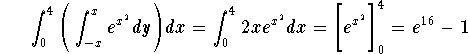
Hence
Problem 5. Evaluate
Answer. Set
(see the picture below of the set G)
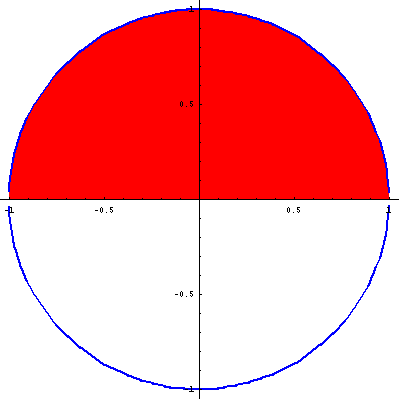
In polar coordinates, we get
Therefore we have
Since
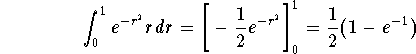
we get
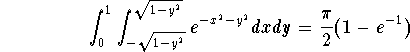
Do you need more help? Please post your question on our
S.O.S. Mathematics CyberBoard.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour
