The Root and Ratio Tests

Here we will discuss the most popular tests of convergence known for series. They are to be used only on positive series.

The Root Test:

Let be a positive series. Assume that

.

Then we have the following:

1.

If , then the series is convergent or;

2.

If , then the series is divergent or;

3.

Iff , then the series may be convergent or it may be divergent. In other words, we do not have a definite conclusion.

The Ratio Test:

Let be a positive series such that for any . Assume that

.

Then we have the following:

1.

If , then the series is convergent or;

2.

If , then the series is divergent or;

3.

If , then the series may be convergent or it may be divergent. In other words, we do not have a definite conclusion.

Remark: What do we mean when we say we do not have a definite conclusion? Simply that one may come up with series for which L=1 (in both tests) and they are convergent and other ones which are divergent.

Example: Use the Ratio and Root Tests for the harmonic series

.

Answer: First, let us take care of the Ratio Test. We have

,

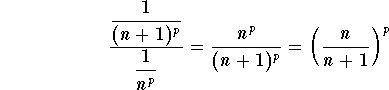which clearly implies

.

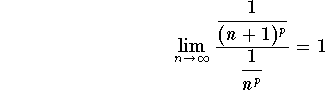Hence, we have L=1.

Next, we consider the Root Test. We have

.

Since

,

then we have

.

Again, we have L=1.

But, we know that is convergent, if and only if, p >1.

Remark: Note that the ratio-test is very appropriate and useful when the series has factorial terms.

Example: Discuss the convergence of

where a > 0.

Answer: Because of the factorial, we will use the Ratio Test. We have

.

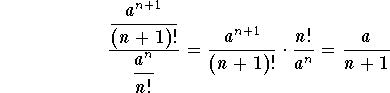Since

,

then the series is convergent.

Note that, in this case, we must have

for any a >0. Moreover, you may wonder what is the total sum? Using the Taylor-series one can show that

.

Example:Discuss the convergence of

.

Answer: Because of the factorial, we will use the Ratio Test. We have

.

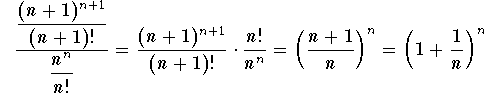Since

then the series is divergent.

For more examples, please click HERE.

[Trigonometry] [Calculus] [Geometry] [Algebra] [Differential Equations] [Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour