More Problems on Series

In this page you will find some not-so-easy problems on sequences. We invite you to solve them and submit the answer to SOS MATHematics. We will publish your answer with your name. Good luck.

Problem 1: Discuss the convergence or divergence of

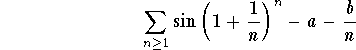displaymath100,

where a and b are two parameters.

Problem 2: Discuss the convergence or divergence of

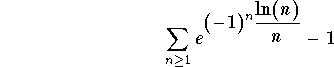displaymath106.

Problem 3: Discuss the convergence or divergence of

displaymath108,

where

displaymath110.

Problem 4: Discuss the convergence or divergence of

displaymath112.

Problem 5: Discuss the convergence or divergence of

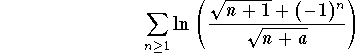displaymath114,

where a > 0.

Problem 6: Duhamel's Rule
Assume that the series tex2html_wrap_inline118 satisfies

displaymath120,

where b is a real number and the function tex2html_wrap_inline124 satisfies

displaymath126.

1.
Show that if b < 1, then the series tex2html_wrap_inline118 is divergent.
2.
Show that if b > 1, then the series tex2html_wrap_inline118 is convergent.
3.
What happens to tex2html_wrap_inline118 if b=1?

Problem 7: Abel's Theorem
Let tex2html_wrap_inline140 and tex2html_wrap_inline142 be two sequences of real numbers such that

1.
there exists M such that for every tex2html_wrap_inline146, we have

displaymath148;

2.
tex2html_wrap_inline150;

3.
the series tex2html_wrap_inline152 is convergent.

Then the series tex2html_wrap_inline154 is convergent.

Problem 8: Discuss the convergence or divergence of

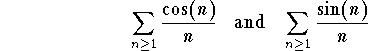displaymath156.

Problem 9: Let tex2html_wrap_inline140 be a sequence of positive decreasing numbers.

1.
Show that the sequence tex2html_wrap_inline160 converges to 0, if the series tex2html_wrap_inline118 converges. What about the converse?;
2.
Set

displaymath164

Is there a relationship between convergence of tex2html_wrap_inline166 and tex2html_wrap_inline168 ?;

3.
Assume that tex2html_wrap_inline170 is convergent. What can you say about tex2html_wrap_inline172 ?

Problem 10: Let tex2html_wrap_inline166 be a divergent series of positive numbers. Discuss the convergence or divergence of the following series:

displaymath176

where tex2html_wrap_inline178 .

Problem 11: Discuss the convergence or divergence of

displaymath180.

Problem 12: Discuss the convergence or divergence of

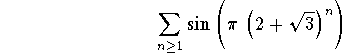displaymath182.

Problem 13: Discuss the convergence or divergence of

displaymath184,

where a is a real number.

Problem 14: Discuss the convergence or divergence of

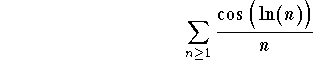displaymath188.

[Trigonometry] [Calculus]
[Geometry] [Algebra] [Differential Equations]
[Calculus] [Complex Variables] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Mohamed A. Khamsi
Tue Dec 3 17:39:00 MST 1996

Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour