Trigonometric Substitutions: Example 2
Trigonometric Substitutions: Example 2
Evaluate
Solution. First let us
complete the square
for 
. We get
which suggests the secant-substitution 
. Hence
we have 
and 
. Note that for x=0, we have 
which gives
t=0 and for x=3, we have 
which gives 
.
Therefore, we have
Using the trigonometric identities (you will find them at the end of this page), we get
The technique of integration related to the powers of the
secant-function gives 
and
which implies
One would check easily that
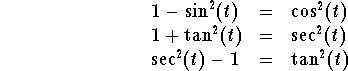
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.
Author: Mohamed Amine Khamsi