 Techniques of Integration: Substitution-Example 2
Techniques of Integration: Substitution-Example 2 Techniques of Integration: Substitution-Example 2
Techniques of Integration: Substitution-Example 2

Evaluate
![]()
Solution. It is clear by looking at the
given integral, that the major problem will be to handle ![]() and
and
![]() . Indeed, it is always harder to handle the nth-root
functions when it comes to integration. Therefore a good substitution
will be to take care of both root-functions at the same time. For
example, we may choose
. Indeed, it is always harder to handle the nth-root
functions when it comes to integration. Therefore a good substitution
will be to take care of both root-functions at the same time. For
example, we may choose ![]() which will make
which will make ![]() and
and ![]() polynomial functions of u. For example, one
may take n = 36 which will give
polynomial functions of u. For example, one
may take n = 36 which will give
![]()
Clearly we are generating a rational function of u which will take a lot of work to handle. This leads us to reconsider the choice of n and try to make it as small as possible. The right choice will be n=6 which the least common factor of 2 and 3. In this case we have
![]()
The method of partial fractions gives
![]()
which gives
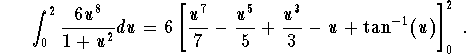
Hence we get
![]()

 S.O.S MATHematics home page
S.O.S MATHematics home page Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Author: Mohamed Amine Khamsi