Solving Logarithmic Equations

We want to find the solutions to

log(8x) - log(1 + $\displaystyle \sqrt{x}$) = 2.

Let us note that the equation is only defined when the input for the logarithms is positive. Thus we need x > 0 and 1 + $ \sqrt{x}$ > 0. Since the second condition is automatically satisfied when x > 0, the equation is defined for all positive x.

We begin by combining the two logarithmic expressions into one expression, using the rule that

log$\displaystyle \left(\vphantom{\frac{a}{b}}\right.$$\displaystyle {\frac{a}{b}}$$\displaystyle \left.\vphantom{\frac{a}{b}}\right)$ = log a - log b.

Consequently our equation becomes

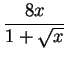
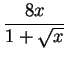log$\displaystyle \left(\vphantom{\frac{8x}{1+\sqrt{x}}}\right.$$\displaystyle {\frac{8x}{1+\sqrt{x}}}$$\displaystyle \left.\vphantom{\frac{8x}{1+\sqrt{x}}}\right)$ = 2.

This is equivalent to saying that

$\displaystyle {\frac{8x}{1+\sqrt{x}}}$ = 102 = 100

Next we multiply both sides by the denominator on the left:

8x = 100(1 + $\displaystyle \sqrt{x}$),

or equivalently

8x - 100 = 100$\displaystyle \sqrt{x}$.

Next we square both sides to eliminate the square root term:

(8x - 100)2 = 10, 000x $\displaystyle \Leftrightarrow$  64x2 - 1, 600x + 10, 000 = 10, 000x.

Simplifying we obtain the quadratic equation

8x2 - 1, 450x + 1, 250 = 0.

Using the quadratic formula, we compute two solutions to this quadratic equation as

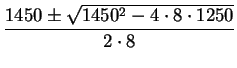x = $\displaystyle {\frac{1450\pm\sqrt{1450^2-4\cdot8\cdot1250}}{2\cdot8}}$.

Numerically the solutions equal x1 $ \approx$ 180.383 and x2 $ \approx$ 0.86621.

It is essential that you now check both answers in the original equation!

For x1,

log(8x1) - log(1 + $\displaystyle \sqrt{x_1}$) $\displaystyle \approx$ 2.000,

thus x1 is a solution to the equation.

On the other hand,

log(8x2) - log(1 + $\displaystyle \sqrt{x_2}$) $\displaystyle \approx$ .555,

thus x2 is not a solution to the equation.

Answer: The equation has exactly one solution, namely

x = $\displaystyle {\frac{1450+\sqrt{1450^2-4\cdot8\cdot1250}}{2\cdot8}}$ $\displaystyle \approx$ 180.383.

[Back to Rules of Logarithms] [Back to Exponential Functions]

[Algebra]
[Algebra] [Trigonometry] [Complex Variables]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Helmut Knaust

Copyright © 1999-2025 MathMedics, LLC. All rights reserved.
Contact us
Math Medics, LLC. - P.O. Box 12395 - El Paso TX 79913 - USA
users online during the last hour