Factoring over the Complex Numbers, Answer 6

Exercise 6.

(a) Show that every polynomial of degree 3 has at least one x-intercept.

(b) Give an example of a polynomial of degree 4 without any x-intercepts.

Answer.

(a) Since complex roots show up in pairs, not all 3 roots can be complex, so at least one of them must be real! Or: Go back to your solution of Exercise 5. Every case has at least one real root.

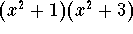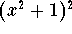(b) Now it can happen that all roots are complex! The polynomials and are such examples.

[Back] [Exercises] [Next] [Algebra] [Trigonometry] [Complex Variables] [Calculus] [Differential Equations] [Matrix Algebra]

S.O.S MATHematics home page

Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard.

Helmut Knaust
Tue Jun 24 09:52:49 MDT 1997